Computes the actual and predicted effectiveness of the collection of algorithms.
effectiveness_crm.RdThis function computes the actual and predicted effectiveness of the collection of algorithms for different tolerance values.
effectiveness_crm(model)
# S3 method for effectivenesscrm
autoplot(object, plottype = 1, ...)Arguments
- model
The output of the function cirtmodel.
- object
For autoplot: The output of the function effectiveness_crm
- plottype
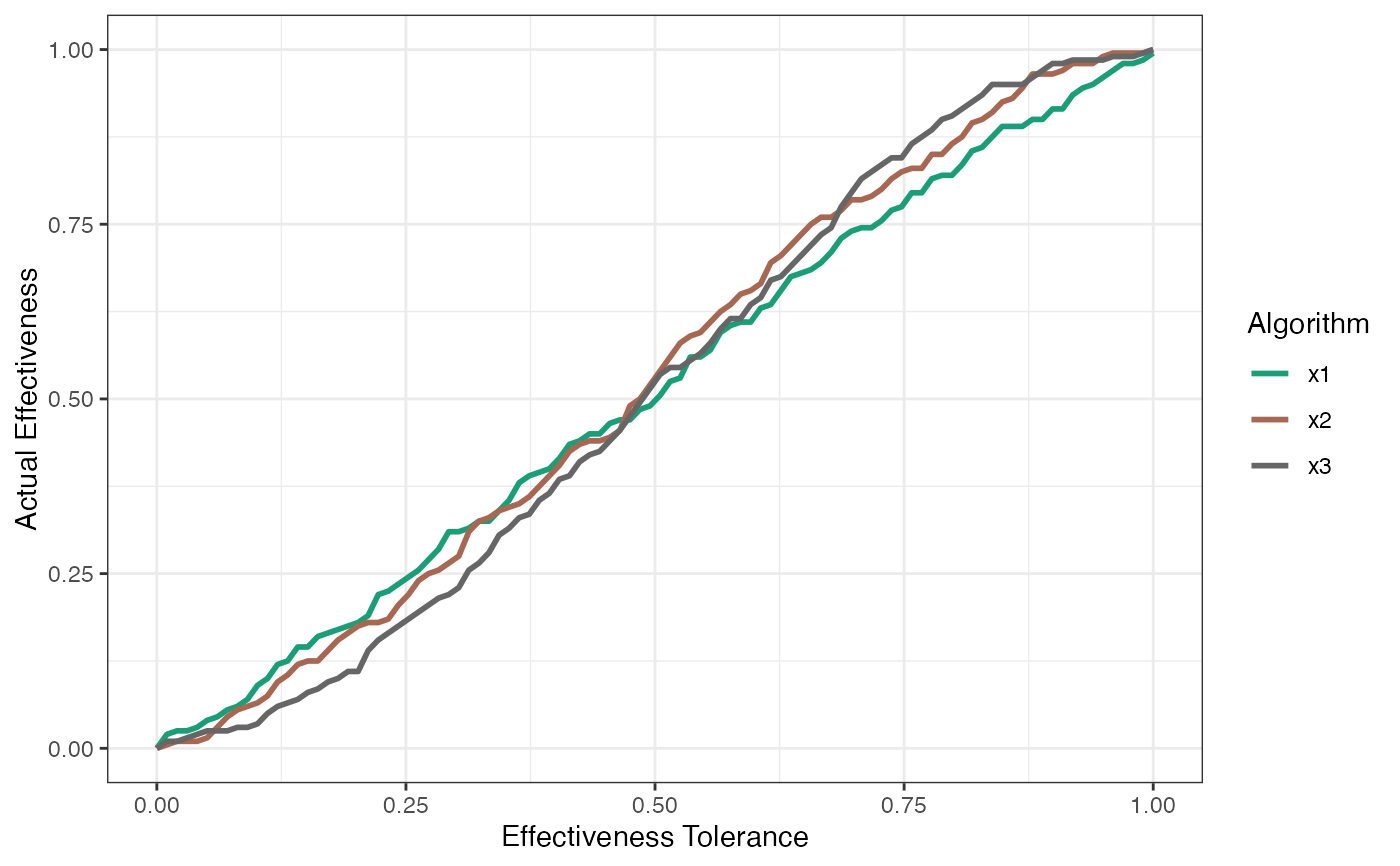
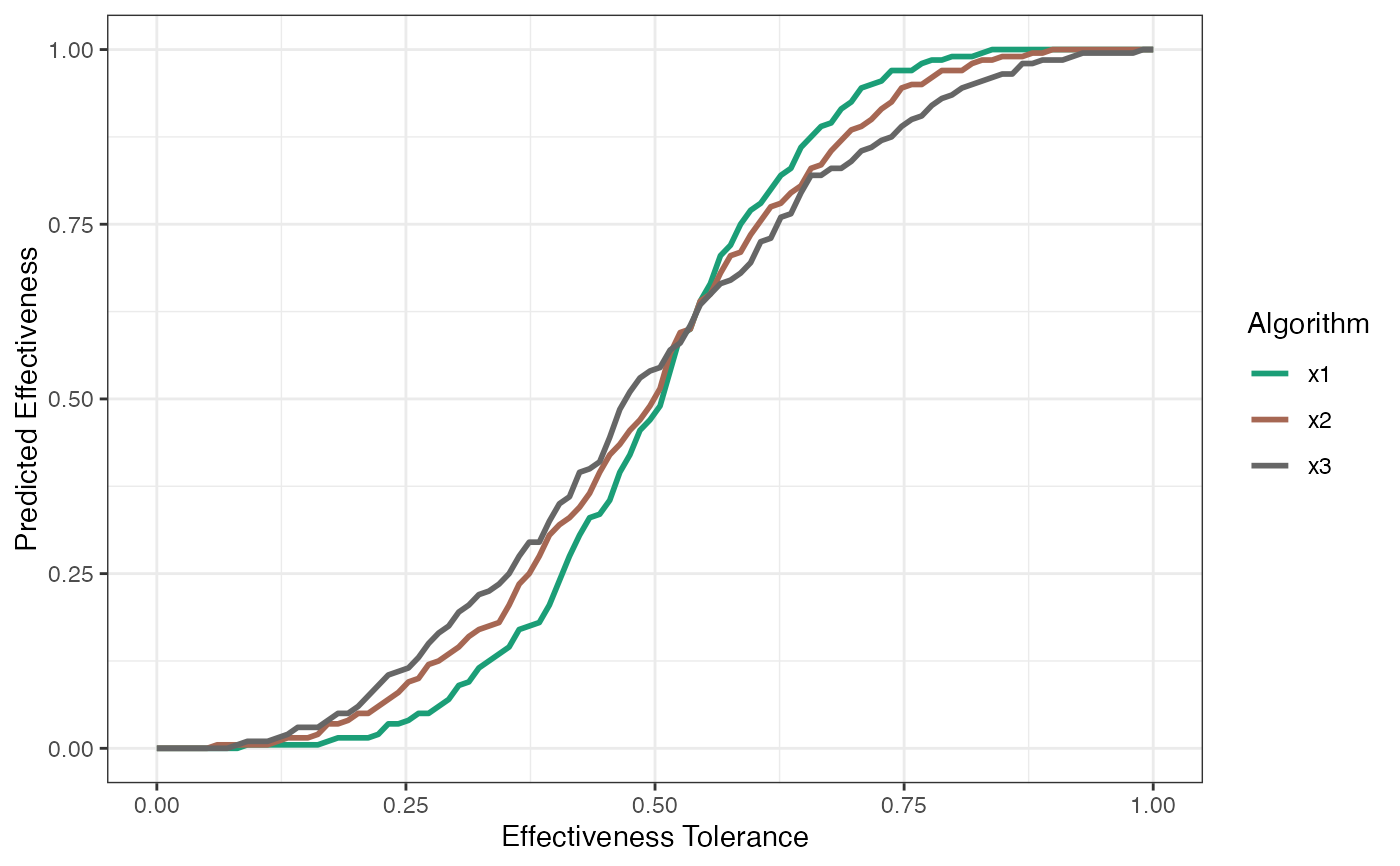
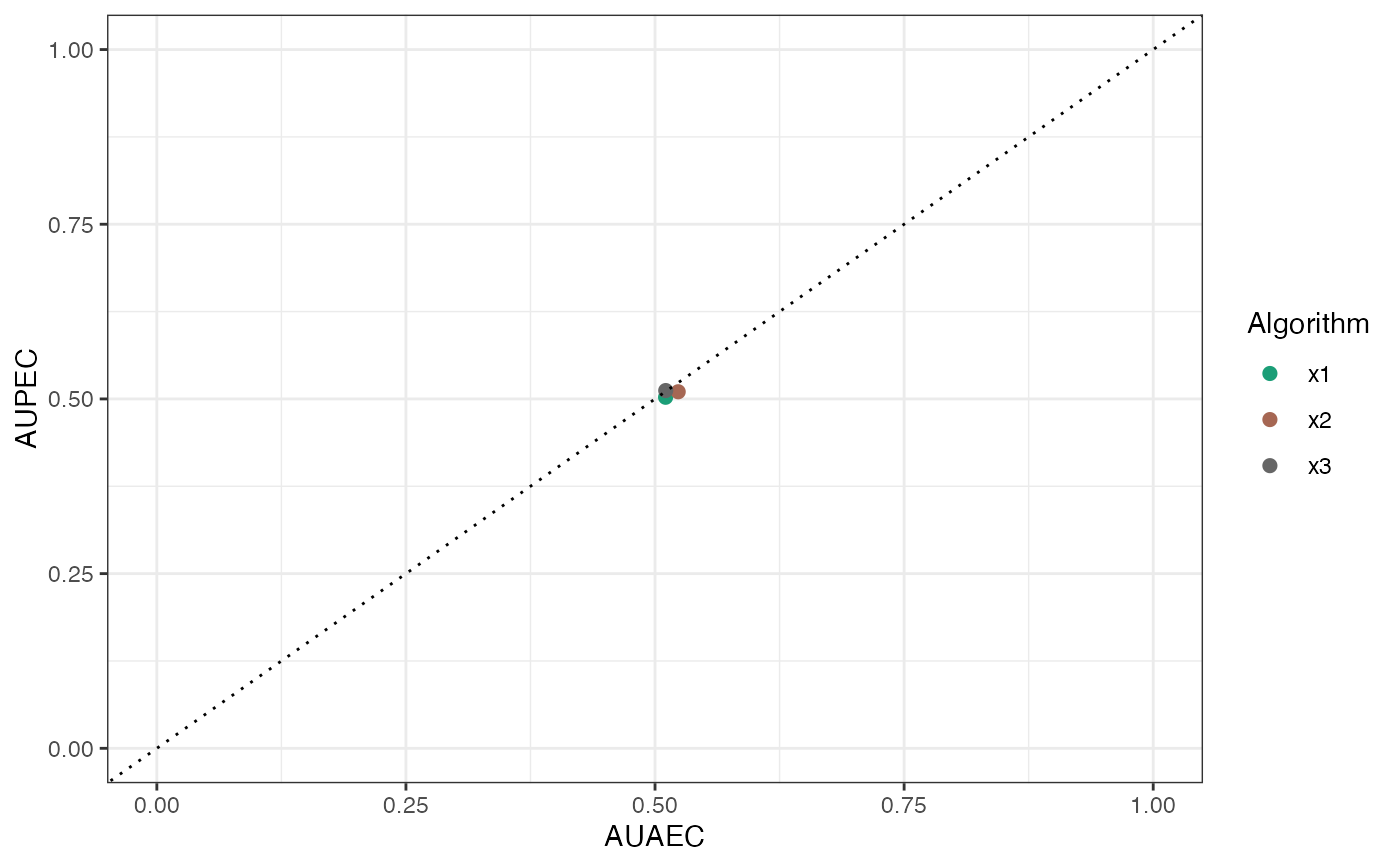
For autoplot: If plottype = 1, then actual effectiveness is plotted, if plottype = 2, then predicted effectiveness is plotted. If plottype = 3, area under the actual effectiveness curve (AUAEC) is plotted against area under the predicted effectiveness curve (AUPEC).
- ...
Other arguments currently ignored.
Value
A list with the following components:
effectivenessAUCThe area under the actual and predicted effectiveness curves.
actcurvesThe
x,ycoodinates for the actual effectiveness curves for each algorithm.
#'
prdcurvesThe
x,ycoodinates for the predicted effectiveness curves for each algorithm.
Examples
set.seed(1)# \donttest{
x1 <- runif(200)
x2 <- 2*x1 + rnorm(200, mean=0, sd=0.1)
x3 <- 1 - x1 + rnorm(200, mean=0, sd=0.1)
X <- cbind.data.frame(x1, x2, x3)
mod <- cirtmodel(X, scale = TRUE, scale.method = "multiple")
out <- effectiveness_crm(mod)
out
#> $effectivenessAUC
#> Actual Predicted
#> x1 0.5106313 0.5022222
#> x2 0.5232323 0.5107071
#> x3 0.5107071 0.5119697
#>
#> $actcurves
#> x x1 x2 x3
#> [1,] 0.00000000 0.000 0.000 0.000
#> [2,] 0.01010101 0.020 0.005 0.010
#> [3,] 0.02020202 0.025 0.010 0.010
#> [4,] 0.03030303 0.025 0.010 0.015
#> [5,] 0.04040404 0.030 0.010 0.020
#> [6,] 0.05050505 0.040 0.015 0.025
#> [7,] 0.06060606 0.045 0.030 0.025
#> [8,] 0.07070707 0.055 0.045 0.025
#> [9,] 0.08080808 0.060 0.055 0.030
#> [10,] 0.09090909 0.070 0.060 0.030
#> [11,] 0.10101010 0.090 0.065 0.035
#> [12,] 0.11111111 0.100 0.075 0.050
#> [13,] 0.12121212 0.120 0.095 0.060
#> [14,] 0.13131313 0.125 0.105 0.065
#> [15,] 0.14141414 0.145 0.120 0.070
#> [16,] 0.15151515 0.145 0.125 0.080
#> [17,] 0.16161616 0.160 0.125 0.085
#> [18,] 0.17171717 0.165 0.140 0.095
#> [19,] 0.18181818 0.170 0.155 0.100
#> [20,] 0.19191919 0.175 0.165 0.110
#> [21,] 0.20202020 0.180 0.175 0.110
#> [22,] 0.21212121 0.190 0.180 0.140
#> [23,] 0.22222222 0.220 0.180 0.155
#> [24,] 0.23232323 0.225 0.185 0.165
#> [25,] 0.24242424 0.235 0.205 0.175
#> [26,] 0.25252525 0.245 0.220 0.185
#> [27,] 0.26262626 0.255 0.240 0.195
#> [28,] 0.27272727 0.270 0.250 0.205
#> [29,] 0.28282828 0.285 0.255 0.215
#> [30,] 0.29292929 0.310 0.265 0.220
#> [31,] 0.30303030 0.310 0.275 0.230
#> [32,] 0.31313131 0.315 0.310 0.255
#> [33,] 0.32323232 0.325 0.325 0.265
#> [34,] 0.33333333 0.325 0.330 0.280
#> [35,] 0.34343434 0.340 0.340 0.305
#> [36,] 0.35353535 0.355 0.345 0.315
#> [37,] 0.36363636 0.380 0.350 0.330
#> [38,] 0.37373737 0.390 0.360 0.335
#> [39,] 0.38383838 0.395 0.375 0.355
#> [40,] 0.39393939 0.400 0.390 0.365
#> [41,] 0.40404040 0.415 0.405 0.385
#> [42,] 0.41414141 0.435 0.425 0.390
#> [43,] 0.42424242 0.440 0.435 0.410
#> [44,] 0.43434343 0.450 0.440 0.420
#> [45,] 0.44444444 0.450 0.440 0.425
#> [46,] 0.45454545 0.465 0.445 0.440
#> [47,] 0.46464646 0.470 0.455 0.455
#> [48,] 0.47474747 0.470 0.490 0.475
#> [49,] 0.48484848 0.485 0.500 0.495
#> [50,] 0.49494949 0.490 0.520 0.515
#> [51,] 0.50505051 0.505 0.540 0.535
#> [52,] 0.51515152 0.525 0.560 0.545
#> [53,] 0.52525253 0.530 0.580 0.545
#> [54,] 0.53535354 0.560 0.590 0.555
#> [55,] 0.54545455 0.560 0.595 0.565
#> [56,] 0.55555556 0.570 0.610 0.580
#> [57,] 0.56565657 0.595 0.625 0.600
#> [58,] 0.57575758 0.605 0.635 0.615
#> [59,] 0.58585859 0.610 0.650 0.615
#> [60,] 0.59595960 0.610 0.655 0.635
#> [61,] 0.60606061 0.630 0.665 0.645
#> [62,] 0.61616162 0.635 0.695 0.670
#> [63,] 0.62626263 0.655 0.705 0.675
#> [64,] 0.63636364 0.675 0.720 0.690
#> [65,] 0.64646465 0.680 0.735 0.705
#> [66,] 0.65656566 0.685 0.750 0.720
#> [67,] 0.66666667 0.695 0.760 0.735
#> [68,] 0.67676768 0.710 0.760 0.745
#> [69,] 0.68686869 0.730 0.770 0.775
#> [70,] 0.69696970 0.740 0.785 0.795
#> [71,] 0.70707071 0.745 0.785 0.815
#> [72,] 0.71717172 0.745 0.790 0.825
#> [73,] 0.72727273 0.755 0.800 0.835
#> [74,] 0.73737374 0.770 0.815 0.845
#> [75,] 0.74747475 0.775 0.825 0.845
#> [76,] 0.75757576 0.795 0.830 0.865
#> [77,] 0.76767677 0.795 0.830 0.875
#> [78,] 0.77777778 0.815 0.850 0.885
#> [79,] 0.78787879 0.820 0.850 0.900
#> [80,] 0.79797980 0.820 0.865 0.905
#> [81,] 0.80808081 0.835 0.875 0.915
#> [82,] 0.81818182 0.855 0.895 0.925
#> [83,] 0.82828283 0.860 0.900 0.935
#> [84,] 0.83838384 0.875 0.910 0.950
#> [85,] 0.84848485 0.890 0.925 0.950
#> [86,] 0.85858586 0.890 0.930 0.950
#> [87,] 0.86868687 0.890 0.945 0.950
#> [88,] 0.87878788 0.900 0.965 0.960
#> [89,] 0.88888889 0.900 0.965 0.970
#> [90,] 0.89898990 0.915 0.965 0.980
#> [91,] 0.90909091 0.915 0.970 0.980
#> [92,] 0.91919192 0.935 0.980 0.985
#> [93,] 0.92929293 0.945 0.980 0.985
#> [94,] 0.93939394 0.950 0.980 0.985
#> [95,] 0.94949495 0.960 0.990 0.985
#> [96,] 0.95959596 0.970 0.995 0.990
#> [97,] 0.96969697 0.980 0.995 0.990
#> [98,] 0.97979798 0.980 0.995 0.990
#> [99,] 0.98989899 0.985 0.995 0.995
#> [100,] 1.00000000 0.995 1.000 1.000
#>
#> $prdcurves
#> x x1 x2 x3
#> [1,] 0.00000000 0.000 0.000 0.000
#> [2,] 0.01010101 0.000 0.000 0.000
#> [3,] 0.02020202 0.000 0.000 0.000
#> [4,] 0.03030303 0.000 0.000 0.000
#> [5,] 0.04040404 0.000 0.000 0.000
#> [6,] 0.05050505 0.000 0.000 0.000
#> [7,] 0.06060606 0.000 0.005 0.000
#> [8,] 0.07070707 0.000 0.005 0.000
#> [9,] 0.08080808 0.000 0.005 0.005
#> [10,] 0.09090909 0.005 0.005 0.010
#> [11,] 0.10101010 0.005 0.005 0.010
#> [12,] 0.11111111 0.005 0.005 0.010
#> [13,] 0.12121212 0.005 0.010 0.015
#> [14,] 0.13131313 0.005 0.015 0.020
#> [15,] 0.14141414 0.005 0.015 0.030
#> [16,] 0.15151515 0.005 0.015 0.030
#> [17,] 0.16161616 0.005 0.020 0.030
#> [18,] 0.17171717 0.010 0.035 0.040
#> [19,] 0.18181818 0.015 0.035 0.050
#> [20,] 0.19191919 0.015 0.040 0.050
#> [21,] 0.20202020 0.015 0.050 0.060
#> [22,] 0.21212121 0.015 0.050 0.075
#> [23,] 0.22222222 0.020 0.060 0.090
#> [24,] 0.23232323 0.035 0.070 0.105
#> [25,] 0.24242424 0.035 0.080 0.110
#> [26,] 0.25252525 0.040 0.095 0.115
#> [27,] 0.26262626 0.050 0.100 0.130
#> [28,] 0.27272727 0.050 0.120 0.150
#> [29,] 0.28282828 0.060 0.125 0.165
#> [30,] 0.29292929 0.070 0.135 0.175
#> [31,] 0.30303030 0.090 0.145 0.195
#> [32,] 0.31313131 0.095 0.160 0.205
#> [33,] 0.32323232 0.115 0.170 0.220
#> [34,] 0.33333333 0.125 0.175 0.225
#> [35,] 0.34343434 0.135 0.180 0.235
#> [36,] 0.35353535 0.145 0.205 0.250
#> [37,] 0.36363636 0.170 0.235 0.275
#> [38,] 0.37373737 0.175 0.250 0.295
#> [39,] 0.38383838 0.180 0.275 0.295
#> [40,] 0.39393939 0.205 0.305 0.325
#> [41,] 0.40404040 0.240 0.320 0.350
#> [42,] 0.41414141 0.275 0.330 0.360
#> [43,] 0.42424242 0.305 0.345 0.395
#> [44,] 0.43434343 0.330 0.365 0.400
#> [45,] 0.44444444 0.335 0.395 0.410
#> [46,] 0.45454545 0.355 0.420 0.445
#> [47,] 0.46464646 0.395 0.435 0.485
#> [48,] 0.47474747 0.420 0.455 0.510
#> [49,] 0.48484848 0.455 0.470 0.530
#> [50,] 0.49494949 0.470 0.490 0.540
#> [51,] 0.50505051 0.490 0.515 0.545
#> [52,] 0.51515152 0.540 0.565 0.570
#> [53,] 0.52525253 0.590 0.595 0.580
#> [54,] 0.53535354 0.600 0.600 0.605
#> [55,] 0.54545455 0.640 0.640 0.635
#> [56,] 0.55555556 0.665 0.650 0.650
#> [57,] 0.56565657 0.705 0.680 0.665
#> [58,] 0.57575758 0.720 0.705 0.670
#> [59,] 0.58585859 0.750 0.710 0.680
#> [60,] 0.59595960 0.770 0.735 0.695
#> [61,] 0.60606061 0.780 0.755 0.725
#> [62,] 0.61616162 0.800 0.775 0.730
#> [63,] 0.62626263 0.820 0.780 0.760
#> [64,] 0.63636364 0.830 0.795 0.765
#> [65,] 0.64646465 0.860 0.805 0.795
#> [66,] 0.65656566 0.875 0.830 0.820
#> [67,] 0.66666667 0.890 0.835 0.820
#> [68,] 0.67676768 0.895 0.855 0.830
#> [69,] 0.68686869 0.915 0.870 0.830
#> [70,] 0.69696970 0.925 0.885 0.840
#> [71,] 0.70707071 0.945 0.890 0.855
#> [72,] 0.71717172 0.950 0.900 0.860
#> [73,] 0.72727273 0.955 0.915 0.870
#> [74,] 0.73737374 0.970 0.925 0.875
#> [75,] 0.74747475 0.970 0.945 0.890
#> [76,] 0.75757576 0.970 0.950 0.900
#> [77,] 0.76767677 0.980 0.950 0.905
#> [78,] 0.77777778 0.985 0.960 0.920
#> [79,] 0.78787879 0.985 0.970 0.930
#> [80,] 0.79797980 0.990 0.970 0.935
#> [81,] 0.80808081 0.990 0.970 0.945
#> [82,] 0.81818182 0.990 0.980 0.950
#> [83,] 0.82828283 0.995 0.985 0.955
#> [84,] 0.83838384 1.000 0.985 0.960
#> [85,] 0.84848485 1.000 0.990 0.965
#> [86,] 0.85858586 1.000 0.990 0.965
#> [87,] 0.86868687 1.000 0.990 0.980
#> [88,] 0.87878788 1.000 0.995 0.980
#> [89,] 0.88888889 1.000 0.995 0.985
#> [90,] 0.89898990 1.000 1.000 0.985
#> [91,] 0.90909091 1.000 1.000 0.985
#> [92,] 0.91919192 1.000 1.000 0.990
#> [93,] 0.92929293 1.000 1.000 0.995
#> [94,] 0.93939394 1.000 1.000 0.995
#> [95,] 0.94949495 1.000 1.000 0.995
#> [96,] 0.95959596 1.000 1.000 0.995
#> [97,] 0.96969697 1.000 1.000 0.995
#> [98,] 0.97979798 1.000 1.000 0.995
#> [99,] 0.98989899 1.000 1.000 1.000
#> [100,] 1.00000000 1.000 1.000 1.000
#>
#> $call
#> effectiveness_crm(model = mod)
#>
#> attr(,"class")
#> [1] "effectivenesscrm"
# For the actual effectiveness plot
autoplot(out, plottype = 1)
 # For the predicted effectivness plot
autoplot(out, plottype = 2)
# For the predicted effectivness plot
autoplot(out, plottype = 2)
 # For actual and predicted effectiveness plot
autoplot(out, plottype = 3)
# For actual and predicted effectiveness plot
autoplot(out, plottype = 3)
 # }
# }